0.1.5

pytorch04

September 22, 2017

woobamboo

关系拟合(回归)

这次将见证如何通过简单的形式将一群数据用一条线段来表示。

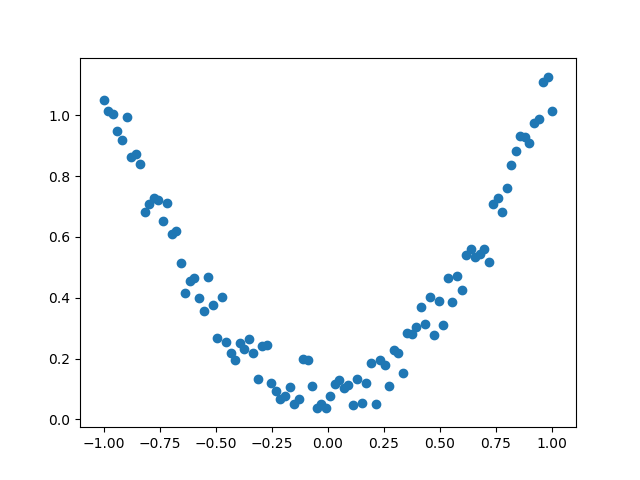
建立数据集

import torch
from torch.autograd import Variable
import matplotlib.pyplot as plt

x = torch.unsqueeze(torch.linspace(-1, 1, 100), dim=1)  # x data (tensor), shape=(100, 1)
y = x.pow(2) + 0.2*torch.rand(x.size())                 # noisy y data (tensor), shape=(100, 1)

# 用 Variable 来修饰这些数据 tensor
x, y = torch.autograd.Variable(x), Variable(y)

# 画图
plt.scatter(x.data.numpy(), y.data.numpy())
plt.show()

unsequeeze函数之后，变成了[[1,2,3,4,5]]这样的结构

建立神经网络

先定义所有的层属性(__init__()), 然后再一层层搭建(forward(x))层于层的关系链接.

import torch
import torch.nn.functional as F     # 激励函数都在这

class Net(torch.nn.Module):  # 继承 torch 的 Module
    def __init__(self, n_feature, n_hidden, n_output):
        super(Net, self).__init__()     # 继承 __init__ 功能
        # 定义每层用什么样的形式
        self.hidden = torch.nn.Linear(n_feature, n_hidden)   # 隐藏层线性输出
        self.predict = torch.nn.Linear(n_hidden, n_output)   # 输出层线性输出

    def forward(self, x):   # 这同时也是 Module 中的 forward 功能
        # 正向传播输入值, 神经网络分析出输出值
        x = F.relu(self.hidden(x))      # 激励函数(隐藏层的线性值)
        x = self.predict(x)             # 输出值
        return x


net = Net(n_feature=1, n_hidden=10, n_output=1)

print(net)  # net 的结构

"""
Net (
  (hidden): Linear (1 -> 10)
  (predict): Linear (10 -> 1)
)
"""

训练网络

训练的步骤很简单, 如下:

# optimizer 是训练的工具
optimizer = torch.optim.SGD(net.parameters(), lr=0.5)  # 传入 net 的所有参数, 学习率.优化器优化神经网络的参数，并传入学习率。
loss_func = torch.nn.MSELoss()      # 预测值和真实值的误差计算公式 (均方差)

for t in range(100):
    prediction = net(x)     # 喂给 net 训练数据 x, 输出预测值

    loss = loss_func(prediction, y)     # 计算两者的误差

    optimizer.zero_grad()   # 清空上一步的残余更新参数值
    loss.backward(retain_graph=True)         # 误差反向传播, 计算参数更新值 参数说明见下面。
    optimizer.step()        # 将参数更新值施加到 net 的 parameters 上

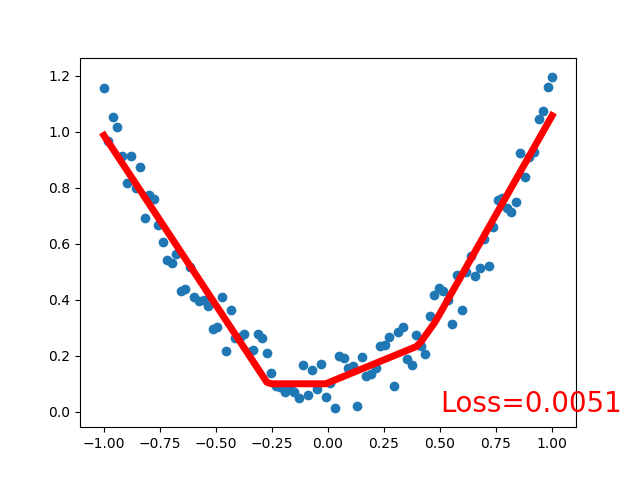
可视化训练过程

import matplotlib.pyplot as plt

plt.ion()   # 画图，变成一个实时打印的过程。
plt.show()

for t in range(100):

    ...
    loss.backward(retain_graph=True)
    optimizer.step()

    # 接着上面来
    if t % 5 == 0:
        # plot and show learning process
        plt.cla()
        plt.scatter(x.data.numpy(), y.data.numpy())
        plt.plot(x.data.numpy(), prediction.data.numpy(), 'r-', lw=5)
        plt.text(0.5, 0, 'Loss=%.4f' % loss.data[0], fontdict={'size': 20, 'color':  'red'})
        plt.pause(0.1)

pytorch_tutorials_By default, gradient computation flushes all the internal buffers contained in the graph, so if you even want to do the backward on some part of the graph twice, you need to pass in retain_variables = True during the first pass.

Recent posts